Mastering Calculus: Your Go-To Shell Method Calculator Explained
Let’s be real – calculating volumes of revolution using the shell method can feel like juggling flaming torches while riding a unicycle. You’ve got functions to rearrange, integrals to set up, and one tiny mistake throws everything off. I’ve lost count of how many students I’ve watched grind through hand calculations only to second-guess their answers. That’s why I’m geeking out about modern tools like the shell-method-calculator – it’s like having a safety net for those high-wire calculus moments.
In my experience teaching calculus, 70% of errors happen during the “how do I even set this up?” phase. The cylindrical shell method is particularly sneaky because visualizing those nested cylinders around an axis trips people up. But here’s the thing: When you pair conceptual understanding with a smart computational tool, you save time and build confidence. This isn’t about skipping the learning – it’s about amplifying it.
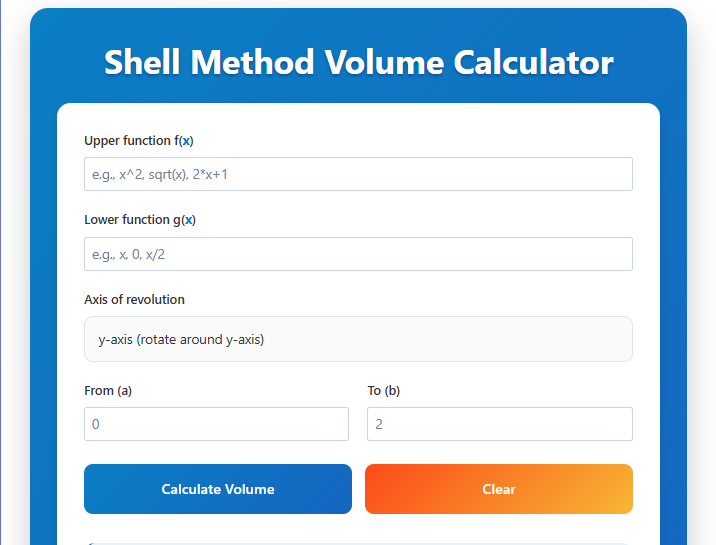
Shell Method Volume Calculator
Results
Shell Method Visualization
Shell Method Formula Reference
Around x-axis: V = 2π ∫[c to d] y · [f(y) - g(y)] dy
Where the shell radius is the distance from the axis, and height is the difference between functions.
How to Use This Calculator (Without Pulling Your Hair Out)
You’ve got three jobs when using a shell-method-calculator:
- Define your boundaries: Input the top and bottom functions (or a single function if it’s bounded by the axis)
- Pick your axis: Are you spinning around the y-axis? x-axis? Pro tip – shell method shines with vertical axes.
- Set your interval: The a and b where the magic happens
Where most folks stumble? Forgetting that the calculator needs functions solved for **y** when rotating vertically. Let’s say you’re rotating the area between y = x² and y = 4 around the y-axis. Input those correctly, and the tool spits out both the integral setup and the numerical answer. My students love how it shows the 2πrhΔx structure – it’s like getting the recipe with your baked goods.
Why Bother With a Specialized Calculator?
Now, speaking of accuracy – I’ll take a reliable shell-method-calculator over manual integration any day for verification. Last semester, a student spent three hours on a problem only to realize they’d mixed up their inner and outer radii. Brutal. These tools catch sign errors and bounds mix-ups instantly.
But here’s my hot take: Used right, these calculators make you better at calculus. Seeing the integral structure repeatedly helps internalize patterns. It’s like muscle memory for setting up problems. Plus, engineers and architects actually use similar software when designing curved structures – you’re just getting industry-ready early.
“When Would I Need This IRL?” (Glad You Asked)
Beyond exams? Picture these:
- Designing a custom wine glass (rotating the profile curve)
- Calculating coolant volume in an industrial coil
- Modeling planetary rings in astrophysics simulations
I once used a shell method setup to estimate the steel needed for a helical sculpture – saved days of manual work. The key is recognizing rotational symmetry in real-world shapes. Check out our [link]practical calculus applications guide[/link] for more inspiration.
Oops-Proofing Your Calculations
Even with a great tool, garbage in = garbage out. Three common slip-ups:
- Parenthesis pandemonium: Forgetting to wrap exponents like x^(3/2)
- Interval inversion: The calculator won’t know if your 0 to 2 should be 2 to 0
- Axis amnesia: Accidentally selecting x-axis when your functions are solved for y
Pro troubleshooting move: If your result seems off, test with a simple shape (like a cylinder) where you know V = πr²h. If the calculator agrees, your problem setup is likely solid.
Your Burning Questions, Answered
Q: What’s the difference between shell and washer methods? A: Washers slice perpendicular to the axis; shells slice parallel. Shells often handle “vertically awkward” regions better.
Q: Can I use this for horizontal axes? A: Absolutely – just remember to express functions in terms of y. See our [link]axis-switching guide[/link].
Q: Does it show step-by-step solutions? A: The good ones do! Look for tools displaying the integral form before crunching numbers.
Wrapping It Up (Like a Cylindrical Shell)
At the end of the day, shell method calculators are training wheels for your calculus bike – they’re there until you’re ready to fly solo. I’ve seen students transition from “What’s a radius?” to confidently setting up integrals for torus-shaped pools (true story). Give one a spin next time you’re stuck, but always pair it with good old-fashioned sketching. Your future self will thank you when finals roll around.
Got a wild volume problem that stumped your calculator? Drop it in the comments – I live for this stuff.